Take 2 riders. Rider A is 68kg/180cm, rider B is 88kg/190cm.
Both riders are using the same, top of the line 6.8kg racing bike. Both have the same body fat, same performance level, all are equal in all other things.

Both riders are going to ride up a hill with a power output of 5 watts per kilo. Their average speed will be under 20kmh, so wind drag in this scenario is negligible. Instinctively, you would think that the lighter rider will win the race. We think this because we often see lighter riders winning mountain stages and we jump to the conclusion they have less weight to carry up the hill.

Back to our scenario; without jumping to conclusions lets look at the situation a bit closer.
Both athletes are riding at 5 w/kg, this means that the power output is equal to their weight. So being lighter should have no advantage. Considering this, it seems that both riders should cross the line at the same time. However, there is still one factor being left out.
THE MISSING FACTOR.
The last consideration in this scenario is the ratio of the bike's weight to the riders weight. Both of the riders have the same 6.8kg bike, the UCI minimum weight. For rider A his bike now becomes a 10% dead weight over and above his body weight. Rider B, riding the same bike is only carrying 7.7% extra dead weight. The difference in bike to rider ratio presents the first mathematical difference between the cyclists.

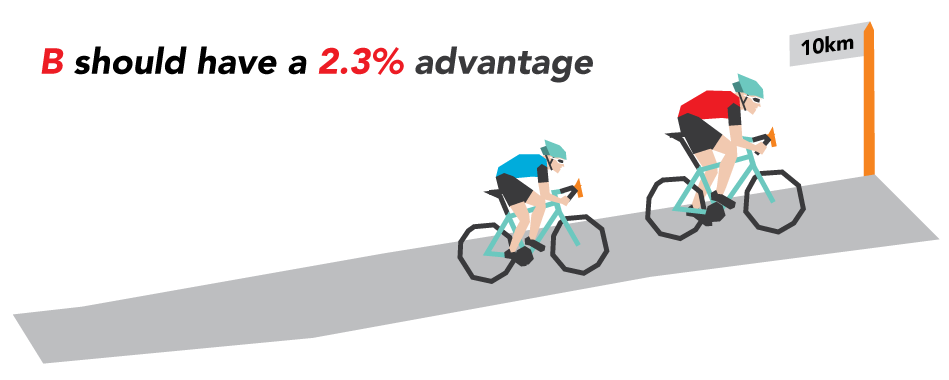
The addition of the bike's weight into the equation shifts the watts per kilo output. Rider A's 10% dead weight compared with Rider B's 7.7%, gives Rider B a 2.3% advantage. This 2.3% advantage gives the heavier rider an additional 23m per kilometre. Over 10km, this will equal a 230m lead over Rider A.
So we've found the difference between the two riders, but it's in the wrong direction. This calculation is in contrast to our initial assumptions about the lighter rider. We've concluded that the heavier rider should have a 230m lead over 10km. Mathematically, the heavier rider should climb 2.3% faster.
IN REALITY.
The real world doesn't reflect the maths we've done. The cyclists we see crossing the line first in mountain stages are the lighter riders, not the Rider Bs of the peloton. If Rider B has the mathematical advantage, then Rider A must have some tricks up his sleeve.
Not sure about you, but Rider B really wants to know what they are.

NEXT WEEK WE'LL TELL YOU WHY RIDER A WILL BEAT B UP THE BERGS.
Please Note: Distances and advantage may vary depending on gradient and calculations used however the concept that Rider B should rider faster remains the evident.
]]>









